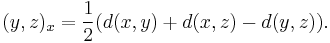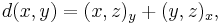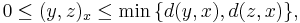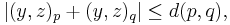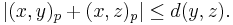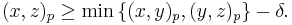Gromov product

In mathematics, the Gromov product is a concept in the theory of metric spaces named after the mathematician Mikhail Gromov. Intuitively, the Gromov product measures the distance for which two geodesics starting at the same point remain "close together". The Gromov product can also be used to define δ-hyperbolic metric spaces in the sense of Gromov.

Definition

Let (X, d) be a metric space and let x, y, z ∈ X. Then the Gromov product of y and z at x, denoted (y, z)_x, is defined by

$(y, z)_{x} = \frac1{2} \big( d(x, y) %2B d(x, z) - d(y, z) \big).$

Properties

The Gromov product is symmetric: (y, z)_x = (z, y)_x.

The Gromov product degenerates at the endpoints: (y, z)_y = (y, z)_z = 0.

For any points p, q, x, y and z,

$d(x, y) = (x, z)_{y} %2B (y, z)_{x},$

$0 \leq (y, z)_{x} \leq \min \big\{ d(y, x), d(z, x) \big\},$

$\big| (y, z)_{p} %2B (y, z)_{q} \big| \leq d(p, q),$

$\big| (x, y)_{p} %2B (x, z)_{p} \big| \leq d(y, z).$

As mentioned in the introduction, the Gromov product measures how long geodesics remain close together. Namely, if x, y and z are three points of a δ-hyperbolic metric space then the initial segments of length (y, z)_x of geodesics from x to y and x to z are no further than 2δ apart (in the sense of the Hausdorff distance between closed sets).

In fact, the Gromov product can be used to define δ-hyperbolic spaces in the sense of Gromov: (X, d) is said to be δ-hyperbolic if, for all p, x, y and z in X,

$(x, z)_{p} \geq \min \big\{ (x, y)_{p}, (y, z)_{p} \big\} - \delta.$

References

Kapovich, Ilya; Benakli, Nadia (2002). "Boundaries of hyperbolic groups". Combinatorial and geometric group theory (New York, 2000/Hoboken, NJ, 2001). Contemp. Math. 296. Providence, RI: Amer. Math. Soc.. pp. 39–93. MR 1921706.
Väisälä, Jussi (2004). "Gromov hyperbolic spaces" (in English) (PDF). http://www.helsinki.fi/~jvaisala/grobok.pdf. Retrieved 2007-08-28.